很多社会、心理研究中所涉及到的变量,都不能准确、直接地测量,这种变量称为潜变量,如工作自主权、工作满意度等。
这时,只能退而求其次,用一些外显指标,去间接测量这些潜变量。如用工作方式选择、工作目标调整作为工作自主权(潜变量)的指标,以目前工作满意度、工作兴趣、工作乐趣、工作厌恶程度(外显指标)作为工作满意度的指标。
传统的统计分析方法不能妥善处理这些潜变量,而结构方程模型则能同时处理潜变量及其指标。
回归分析与结构方程模型
一个回归分析和结构方程比较的例子:
假如有五道题目来测量外向型性格,还有四道题目来测量自信。研究自信与外向型性格的关系。假如是你,你将怎样来进行研究?
回归分析的做法:先分别计算外向题目的总分(或平均分)和自信题目的总分(或平均分),在计算两个总分的相关。
这样的计算所得的两个潜变量(性格与自信)的关系,恰当吗?
线性回归模型及其局限性
1)无法处理因变量(Y)多于一个的情况;
2)无法处理自变量(X)之间的多重共线性;
3)无法对一些不可直接测量的变量进行处理,主要是一些主观性较强的变量进行测量。如幸福感、组织认同感、学习能力等;
4)没有考虑变量(自变量、因变量)的测量误差,以及测量误差之间的关系
多元统计方法中的相关解决方法
针对1):路径分析(Path Analysis)
缺点:分开考察不同的因变量,无法考察因变量之间的关系且缺少整体的视角
针对2):偏最小二乘法(PLS)
缺点:相关理论尚不完善,解释力较弱。
《王惠文,偏最小二乘法理论与应用,国防工业出版社》
针对3):指标赋予权重,进行综合评价,得出一个量化的指标
缺点:权重设计,需要相当的技巧,通常的方法,如AHP,模糊综合评判等方法缺少信度与效度
针对4):没有办法解决
结构方程模型(SEM)的优点
1)同时处理多个因变量
2)容许自变量和因变量含测量误差[传统方法(如回归)假设自变量没有误差]
3)同时估计因子结构和因子关系
4)容许更大弹性的测量模型
5)估计整个模型的拟合程度[用以比较不同模型]
6)SEM包括:回归分析、因子分析(验证性因子分析、 探索性因子分析)、t检验、方差分析、比较各组因子均值、交互作用模型、实验设计
结构方程模型的含义
Structural Equation Model,SEM
Covariance Structure Modeling,CSM
Linear Structural Relationship , LISREL
从上述名称中可以看出,结构方程模型的几个本质特征是:
结构、协方差、线性
结构方程简介
简单来说,结构方程模型分为:
测量方程(measurement equation)测量方程描述潜变量与指标之间的关系,如工作方式选择等指标与工作自主权的关系;
结构方程(structural equation),描述潜变量之间的关系,如工作自主权与工作满意度的关系。
(一)测量模型
对于指标与潜变量(例如两个工作自主权指标与工作自主权)间的关系,通常写为以下测量方程:
•x = Λχ ξ + δ
•y = Λу η + ε
•其中:x——外源指标(如两个工作自主权指标)组成的向量;
• y——内生指标(如四个工作满意度指标)组成的向量;
• ξ——外源潜变量(如工作自主权等)组成的向量;
• η——内生潜变量(如工作满意度等)组成的向量;
• Λχ——外源指标与外源变量之间的关系(如两个工作自主权指标与工作自主权的关系),是外源指标在外源潜变量上的因子负荷矩阵;
• Λу——内生指标与内生变量之间的关系(如四个工作满意度指标与工作满意度的关系),是内生指标在内生潜变量上的因子负荷矩阵;
(二)结构模型
对于潜变量间(如工作自主权与工作满意度)的关系,通常写成如下结构方程:
•η = Β η +Γ ξ + ζ
•其中:B——内生潜变量间的关系(如其它内生潜变量与工作满意度的关系);
• Γ——外源潜变量对内生潜变量的影响(如工作自主权对工作满意度的影响);
• ζ——结构方程的残差项,反映了在方程中未能被解释的部分。
潜变量间的关系,即结构模型,是研究的兴趣重点,所以整个分析也称结构方程模型。
SEM的基本思想与方法
SEM是基于变量的协方差矩阵来分析变量之间关系的一种统计方法,实际上是一般线性模型的拓展,包括因子模型与结构模型,体现了传统路径分析与因子分析的完美结合。 SEM一般使用最大似然法估计模型(Maxi-Likeliheod,ML) 分析结构方程的路径系数等估计值,因为ML法使得研究者能够基于数据分析的结果对模型进行修正。
1、 SEM术语
(1)观测变量 可直接测量的变量,通常是指标
(2)潜变量 潜变量亦称隐变量,是无法直接观测并测量的变量。潜变量需要通过设计若干指标间接加以测量。
(3)外生变量 是指那些在模型或系统中,只起解释变量作用的变量。它们在模型或系统中,只影响其他变量,而不受其他变量的影响。在路径图中,只有指向其他变量的箭头,没有箭头指向它的变量均为外生变量。
(4)内生变量 是指那些在模型或系统中,受模型或系统中其它变量包括外生变量和内生变量影响的变量,即在路径图中,有箭头指向它的变量。它们也可以影响其它变量。
2、结构方程模型示意图
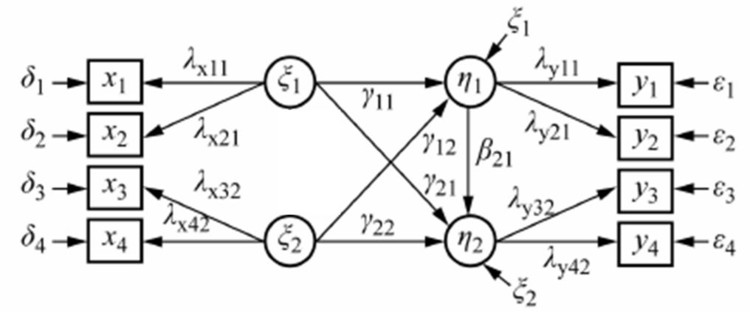
观测变量通常用长方形或方形表示,外生观测变量用x表示,内生观测变量用y表示。 潜变量用椭圆或圆形表示,外生潜变量通常用ξ表示,内生潜变量通常用η表示。 δ外生观测变量x的误差;ε内生观测变量y的误差。
具体过程
1、数据准备
样本量:一般认为样本数最少应在100以上才适合使用最大似然估计法(MLE)来估计结构方程(侯杰泰,2004),但样本数过大(如超过400到500时),MLE会变得过度敏感,容易使所有的拟合度指标检验都出现拟合不佳的结果(侯杰泰,2004)。
缺失数据处理:列删除法、配对删除法、插补法
2、 一般应用SEM的论文中的数据分析
(1).信度、效度检验
信度 Cronbach’s >0.7
效度 验证性因子分析
(2). 评估模型拟合度
即
估算每一个因子的载荷量
标准化因子载荷,反映了观测变量影响潜在变量的部分差异,用于表示观测变量与潜变量之间的相对重要程度。
检查每一个单一因子的测量模型对问卷数据的拟合度
检查整个模型对问卷数据的拟合度
估算潜变量之间的关系
五、 SEM的主要拟合度指标
1、 基本拟合标准
基本拟合标准是用来检验模型的误差以及误输入等问题。
主要包括:
(1)不能有负的测量误差;
(2)测量误差必须达到显著性水平;
(3)因子载荷必须介于0.5-0.95之间;
(4)不能有很大的标准误差。
2、 模型内在结构拟合度
模型的内在结构拟合度是用来评价模型内估计参数的显著程度、各指标及潜在变量的信度。
主要包括:
(1)潜变量的组成信度(CR),0.7以上表明组成信度较好;
潜变量的CR值是其所有观测变量的信度的组合,该指标用来分析潜变量的各观测变量间的一致性
(2)平均提炼方差(AVE),0.5以上为可以接受的水平。
AVE用于估计测量模型的聚合效度,反映了潜变量的各观测变量对该潜变量的平均差异解释力,即潜变量的各观测变量与测量误差相比在多大程度上捕捉到了该潜变量的变化。
3、 整体模型拟合度
整体模型拟合度是用来评价模型与数据的拟合程度。
主要包括:
(1)绝对拟合度,用来确定模型可以预测协方差阵和相关矩阵的程度;
(2)简约拟合度,用来评价模型的简约程度;
(3)增值拟合度,理论模型与虚无模型的比较。
包括
(1)χ2卡方拟合指数 检验选定的模型协方差矩阵与观察数据协方差矩阵相匹配的假设。原假设是模型协方差阵等于样本协方差阵。如果模型拟合的好,卡方值应该不显著。在这种情况下,数据拟合不好的模型被拒绝。
(2)RMR 是残差均方根。RMR 是样本方差和协方差减去对应估计的方差和协方差的平方和,再取平均值的平方根。RMR应该小于0.08,RMR越小,拟合越好。
(3)RMSEA 是近似误差均方根 RMSEA应该小于0.06,越小越好。
GFI 是拟合优度指数,范围在0和1间,但理论上能产生没有意义的负数。按照约定,要接受模型,GFI 应该等于或大于0.90。
(4)PGFI 是简效拟合优度指数。它是简效比率(PRATIO,独立模式的自由度与内定模式的自由度的比率)乘以GFI。 PGFI 应该等于或大于0.90,越接近1越好。
(5)PNFI 是简效拟合优度指数,等于PRATIO乘以 NFI。 PNFI应该等于或大于0.90,越接近1越好。
(6)NFI 是规范拟合指数,变化范围在0和1间, 1 = 完全拟合。按照约定,NFI 小于0.90 表示需要重新设置模型。越接近1越好。
(7)TLI 是Tucker-Lewis 系数,也叫做Bentler-Bonett 非规范拟合指数 (NNFI)。TLI接近1表示拟合良好。
(8)CFI 是比较拟合指数,其值位于0和1之间。CFI 接近1表示拟合非常好,其值大于0.90表示模型可接受,越接近1越好。
六 模型修正
研究者可以参考察初始模型的显著性检验结果和软件(AMOS)提供的模型修正指标对模型进行修正。
(1)模型扩展 添加新路径,提高模型的拟合度
修正指数(modification index)
整个模型改良时卡方值减少
(2)模型限制 删除或限制部分路径,提高模型可识别性
临界比率(Critical ration for difference)
使结果更具有现实性和解释性
版权声明:本文由 Duter2016 在 2019年10月20日发表。本文采用CC BY-NC-SA 4.0许可协议,非商业转载请注明出处,不得用于商业目的。
文章题目及链接:《为何要用结构方程模型?》

